HaskellでB-treeを実装(delete編)
前回に引き続いて今回もHaskellでB-treeの実装。今回はキーの削除を実装する。前回同様 "Introduction to Algorithms" の実装方針に沿って実装する。前回はこちら。
コードはここにおいた
Haskell B-tree implementation · GitHub
shift と merge
キーの削除において重要な概念となるshiftとmergeについてはじめに説明する。B-treeの定義より、各ノードはキーを (m-1) 個以上、 (2m-1) 個以下持たないといけない(m はB-treeのオーダー)。なので、キーを (m-1) 個しか持たないノードからそのままキーを削除することはできない。キーを (m-1) 個しか持たないノードをここでは "few" であると呼ぼう*1。キーを削除する前に、mergeとかshiftといった操作をすることによってノードを予め "few" でない状態にしておく。
まずはshiftについて説明する。shiftにはshift_leftとshift_rightがある。下の図はshift_leftを図示している。左の子ノードは "few" であるため、そこからキーを削除することはできない。そこで、右の子ノード("few" でない)からキーを左に "シフト" することで "few" でない状態にする。ここで注意する点は、そのまま右の子ノードからキーを持ってくるのではなく、右のキーは親ノードへ、親ノードのキーを左の子ノードへシフトする。shift_rightについても同様なので、説明は省く。
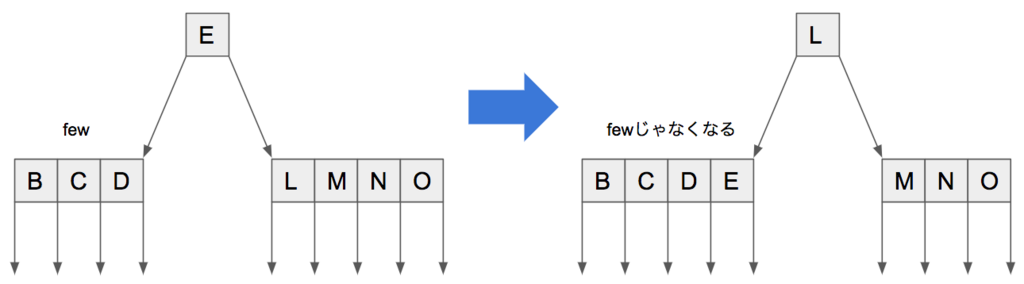
shiftを実装しよう。コードは以下の通り。キーを1つと、その左右の子ノードをそれぞれ引数として受け取り、シフトしてから親ノードを返す。説明したとおりに実装しただけなので、見ればわかると思う。
shift_left :: (Ord a, Eq a) => a -> Tree a -> Tree a -> Tree a shift_left k (Leaf m keys1) (Leaf _ (k2:keys2)) = Node m [k2] [(Leaf m (keys1 ++ [k])), (Leaf m keys2)] shift_left k (Node m keys1 trees1) (Node _ (k2:keys2) (t2:trees2)) = Node m [k2] [(Node m (keys1 ++ [k]) (trees1 ++ [t2])), (Node m keys2 trees2)] shift_right :: (Ord a, Eq a) => a -> Tree a -> Tree a -> Tree a shift_right k (Leaf m keys1) (Leaf _ keys2) = Node m [last keys1] [(Leaf m (init keys1)), (Leaf m (k:keys2))] shift_right k (Node m keys1 trees1) (Node _ keys2 trees2) = Node m [last keys1] [(Node m (init keys1) (init trees1)), (Node m (k:keys2) ((last trees1):trees2))]
mergeについて説明する。いつでもshiftができればいいんだけど、できないときもある。そういうときにmergeが必要となる。ここでも図を使って説明しよう。下の図では左の子ノードが "few" なので、キーを増やしたい。でも隣の子ノードも "few" なのでキーをシフトすることができない。そこで、親ノードの対応するキーも含めて子ノードふたつを "マージ" する。そうすることで、マージされたノードからキーを削除できるようになる。
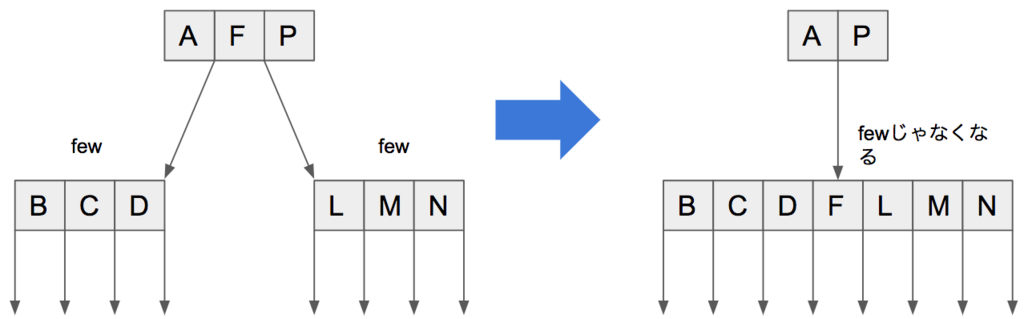
mergeのコードは以下の通り。これも単純で、親ノードのキーと2つの子ノードを受け取って、マージされたノードを返すだけ。引数として渡されたノードがLeafかNodeかで場合分けしているけど、やっていることは本質的には同じ。
merge :: (Ord a, Eq a) => a -> Tree a -> Tree a -> Tree a merge k (Leaf m1 keys1) (Leaf _ keys2) = Leaf m1 (keys1 ++ [k] ++ keys2) merge k (Node m1 keys1 trees1) (Node _ keys2 trees2) = Node m1 (keys1 ++ [k] ++ keys2) (trees1 ++ trees2)
delete の実装
さて、shiftとmergeの説明が終わったので、キーの削除を実装していく。まずはトップレベルの関数deleteを定義する。
delete :: (Ord a, Eq a) => Tree a -> a -> Tree a delete (Nil _) _ = error "Underflow" -- (1) delete (Leaf _ []) _ = error "Underflow" -- (1) delete n@(Node m [k] [t1, t2]) x = if is_few t1 && is_few t2 -- (2) then delete_non_few (merge k t1 t2) x else delete_non_few n x delete n x = delete_non_few n x -- (3)
未定義の関数がいくつも出てきたけど、それらについては順を追って説明する。ここではルートノードの状態に応じて条件分岐しているだけ。それぞれについて見てみよう。(1) 渡された木がNilもしくは空のキーリストを持ったLeafなら削除するキーはもう無いので、エラーを吐く。(2) ルートノードがキーを1つしか持たない(つまり子部分木を2つしか持たない)場合は、子部分木がどちらも "few" ならそれらを mergeしてからdelete_non_fewする。少なくともどちらかが "few" でないなら、そのままdelete_non_fewに渡す。(3) さいごに、ルートノードがキーを2つ以上持つなら、そのときもそのままdelete_non_fewに渡す。
is_fewはノードが "few" であるか否かを判定する関数。以下のように定義する。簡単。
is_few :: (Ord a, Eq a) => Tree a -> Bool is_few (Nil _) = False is_few (Leaf m keys) | length keys == (m - 1) = True | otherwise = False is_few (Node m keys _) | length keys == (m - 1) = True | otherwise = False
メインとなるdelete_non_fewについて見ていこう。この関数に渡されるノードは必ず "few" で無いことが保証されている(というかそうなるように実装する)。定義は以下の通り。
delete_non_few :: (Ord a, Eq a) => Tree a -> a -> Tree a delete_non_few l@(Leaf _ _) x = delete_leaf l x -- (1) delete_non_few n@(Node m [k] [t1, t2]) x -- (2) | x == k = delete_here n x | x < k = delete_middle n x | x > k = delete_last n x delete_non_few n@(Node m (k:ks) (t:t_next:ts)) x -- (3) | x == k = delete_here n x | x < k = delete_middle n x | x > k = Node m (k:new_ks) (t:new_ts) where Node _ new_ks new_ts = delete_non_few (Node m ks (t_next:ts)) x
ここでも3つの場合分けがあるので、それぞれ見てみよう。(1) の場合、つまり渡されたノードがLeafの場合はそのままdelete_leaf(後述)に渡してキーを削除する。(2) は渡されたノードがキーを1つしか持たない場合なんだけど、これは終端処理なので先に (3) を説明しよう。(3) の場合は渡されたノードがキーを2つ以上持つことが保証されている。削除キーxといま注目しているキーkを比較していく。まずx == kの場合は削除すべきキーが見つかったので、nをそのままdelete_here(後述)に渡してキーを削除する。x < kの場合はこのノードnに探しているキーは無いことが分かった、かつ、キーが含まれるべき子部分木も分かったので、delete_middle(後述)で再帰的にキーを削除する。x > kの場合はまだこのノード内にxがある可能性があるので、先頭のキーkを取り除いて残りのキーのリストksに対して再帰的にdelete_non_fewでキーの削除を行う。(3) においてx > kのときの処理を繰り返すことで、いずれ (2) の状態に到達する。
んで、(2) の終端処理もほぼ (3) と同じことをしているんだけど、(2) でx > kになった場合はnの中にキーが無いことが判明、かつ、一番右(最後)の子部分木にキーが含まれるべきであることが判明したので、delete_lastでその子部分木から再帰的にキーを削除する*2。
delete_leafは簡単。delete_leafに渡されてくるノードにキーがあれば単にそれを削除するし、なければ探しているキーxは木全体になかったということになるので、単にlを返して終了する。
delete_leaf :: (Ord a, Eq a) => Tree a -> a -> Tree a delete_leaf l@(Leaf m (k:ks)) x | x == k = Leaf m ks | x < k = l | x > k = Leaf m (k:new_ks) where Leaf _ new_ks = delete_leaf (Leaf m ks) x
次にdelete_hereを見てみよう。ここに渡されてくるノードは、必ずキーのリストの先端kに削除すべきキーを持っていることが保証されている。つまり、delete_hereでは渡されたノードからkを削除する。削除の仕方は二部探索木とほとんど同じで、右(もしくは左)の部分木における最小キー(もしくは最大キー)を削除し、それをkと置き換える。
delete_here :: (Ord a, Eq a) => Tree a -> a -> Tree a delete_here (Node m (k:ks) (t1:t2:ts)) x = if is_few t1 && is_few t2 then Node m ks ((delete_non_few (merge k t1 t2) x):ts) -- (1) else if is_few t1 then Node m ((get_min t2):ks) (t1:(delete_min t2):ts) -- (2) else Node m ((get_max t1):ks) ((delete_max t1):t2:ts) -- (3)
ここも3つの場合分けがあるのでそれぞれ見ていこう。(1) を飛ばして先に (2) と (3) について説明する。(2) ではt1は "few" だけどt2は "few" じゃないので、t2から最小のキーを持ってきて置き換える。(3) では逆にt2は "few" だけどt1は "few" じゃないのでt1から最大のキーを持ってきて置き換える。get_min等の関数については後述。で、(1) のときはt1もt2も "few" なので、それらをmergeしてまた再帰的にdelete_non_fewを呼ぶ。delete_minにもdelete_maxにも "few" のノードを渡さない取り決めにしておくと実装が容易になるのでこうする。
get_min、get_max、delete_min、delete_maxを定義する。これらの関数もシンプルなので特に説明はいらないと思う。get_minとget_maxは渡された部分木の中で最も小さい(大きい)キーを返す。delete_minとdelete_maxはそのキーを削除した部分木を返す。
get_min :: (Ord a, Eq a) => Tree a -> a get_min (Leaf _ keys) = head keys get_min (Node _ _ trees) = get_min (head trees) delete_min :: (Ord a, Eq a) => Tree a -> Tree a delete_min (Leaf m keys) = Leaf m (tail keys) delete_min (Node m keys (t:ts)) = Node m keys ((delete_min t):ts) get_max :: (Ord a, Eq a) => Tree a -> a get_max (Leaf _ keys) = last keys get_max (Node _ _ trees) = get_max (last trees) delete_max :: (Ord a, Eq a) => Tree a -> Tree a delete_max (Leaf m keys) = Leaf m (init keys) delete_max (Node m keys trees) = Node m keys ((init trees) ++ [delete_max (last trees)])
さてさて、長くなってきたけど次はdelete_middleについて見てみよう。この関数では何をするかというと、渡されたノードの中に削除キーxがないことは判明しているので、再帰的に子部分木からキーを削除(delete_non_few)する。削除キーxが含まれるべき子部分木はt1であることは分かっているのでそこに再帰したいんだけど、その前にt1とt2が "few" であるかによってmergeしたりshiftしたりする。mergeしたりshiftしたりすることによってt1は "few" ではなくなるので、安心してdelete_non_fewできる。
delete_middle :: (Ord a, Eq a) => Tree a -> a -> Tree a delete_middle (Node m (k:ks) (t1:t2:ts)) x = if is_few t1 && is_few t2 then Node m ks ((delete_non_few (merge k t1 t2) x):ts) else if is_few t1 then Node m (shifted_k:ks) ((delete_non_few shifted_t1 x):shifted_t2:ts) else Node m (k:ks) ((delete_non_few t1 x):t2:ts) where Node _ [shifted_k] [shifted_t1, shifted_t2] = shift_left k t1 t2
delete_lastはほとんどdelete_middleと同じなんだけど、shift_leftじゃなくてshift_rightする。なぜかというと、もうそれより右の子部分木はないので、そこからshift_leftしてこれないため。delete_lastという名の通り、いま注目しているノードに含まれる子部分木のリストの最後の子部分木に再帰する。それ以外はほとんどdelete_middleと同じことをしている。
delete_last :: (Ord a, Eq a) => Tree a -> a -> Tree a delete_last (Node m [k] [t1, t2]) x = if is_few t2 && is_few t1 then Node m [] [delete_non_few (merge k t1 t2) x] else if is_few t2 then Node m [shifted_k] [shifted_t1, (delete_non_few shifted_t2 x)] else Node m [k] [t1, (delete_non_few t2 x)] where Node _ [shifted_k] [shifted_t1, shifted_t2] = shift_right k t1 t2
以上で実装は終わり。場合分けが結構多いので複雑にはなってしまうんだけど、わかってしまえばやり方は単純で、ほとんど二分探索木のキーの削除と同じ。違うのはノードが "few" になったときにmergeしたりshiftしたりして "few" じゃなくしてからdelete_non_fewに渡すことくらい。その辺の場合分けでややこしくなっている。もっとイケてるかんじの書き方は当然あると思うんだけどあんまりhaskellでB-treeを実装してみたっていう記事がないのでよくわからない。
テスト
簡単にテスト。適当に作ったキーのリストを使ってB-treetを作る。で、その中から適当にキーを削除する。削除したキーをfindするとちゃんとFalseが返って来ていることが分かる。ちゃんと動いてるっぽいね。
*Main> :l btree [1 of 1] Compiling Main ( btree.hs, interpreted ) Ok, one module loaded. *Main> keys = [2,234,746474,235,87876,6,756,65476876,65,658764534,1853,95149,24371,97,1234367252] *Main> t = foldl insert (Nil 2) keys *Main> t Node 2 [87876] [Node 2 [6,234,756] [Leaf 2 [2],Leaf 2 [65,97],Leaf 2 [235],Leaf 2 [1853,24371]],Node 2 [65476876] [Leaf 2 [95149,746474],Leaf 2 [658764534,1234367252]]] *Main> delete t 235 Node 2 [87876] [Node 2 [6,234,1853] [Leaf 2 [2],Leaf 2 [65,97],Leaf 2 [756],Leaf 2 [24371]],Node 2 [65476876] [Leaf 2 [95149,746474],Leaf 2 [658764534,1234367252]]] *Main> find (delete t 235) 235 False *Main> delete t 87876 Node 2 [24371] [Node 2 [6,234,756] [Leaf 2 [2],Leaf 2 [65,97],Leaf 2 [235],Leaf 2 [1853]],Node 2 [65476876] [Leaf 2 [95149,746474],Leaf 2 [658764534,1234367252]]] *Main> find (delete t 87876) 87876 False
HaskellでB-treeを実装
すごいHaskell本を読んだのでなにか練習したいなと思っていたところ、某会*1で「B-treeなんて誰でも簡単に実装できますよね」と煽られたので実装してみた。すごく直感的に書けたので Haskell すごいなーと思った。実装方針は "Introduction to Algorithms" に書いてあるとおり。

- 作者: Miran Lipovača,田中英行,村主崇行
- 出版社/メーカー: オーム社
- 発売日: 2012/05/23
- メディア: 単行本(ソフトカバー)
- 購入: 25人 クリック: 580回
- この商品を含むブログ (73件) を見る

アルゴリズムイントロダクション 第3版 総合版 (世界標準MIT教科書)
- 作者: T.コルメン,R.リベスト,C.シュタイン,C.ライザーソン,Thomas H. Cormen,Clifford Stein,Ronald L. Rivest,Charles E. Leiserson,浅野哲夫,岩野和生,梅尾博司,山下雅史,和田幸一
- 出版社/メーカー: 近代科学社
- 発売日: 2013/12/17
- メディア: 大型本
- この商品を含むブログ (7件) を見る
さっそく実装
B-treeを知っている人を対象にして書きます。B-treeを知らない人は Introduction to Algorithms を読むなりWebでいい感じの記事を探すなりしてね。
コードはここにおいた。
Haskell B-tree implementation · GitHub
まずはデータ型を定義。
data Tree a = Nil Int | Leaf Int [a] | Node Int [a] [Tree a] deriving Show
TreeはNilかLeafかNodeであり、Nodeの中にはまたTreeのリストがあると再帰的に定義されている。Intの部分にはB-treeのオーダーが入る。Leafは保持するキーのリストを持つ。また、Nodeは中間ノードで、保持するキーのリストと保持する部分木のリストを持つ。
キーの検索
次にB-treeからキーを検索する関数を定義。すごく簡単だし直感的に書けるので Haskell かっこいい。
find :: (Ord a, Eq a) => Tree a -> a -> Bool find (Nil _) _ = False find (Leaf _ []) _ = False find (Leaf m (k:ks)) x | x == k = True | x < k = False | x > k = find (Leaf m ks) x find (Node _ [] (t:ts)) x = find t x find (Node m (k:ks) (t:ts)) x | x == k = True | x < k = find t x | x > k = find (Node m ks ts) x
TreeがNilである場合とLeafである場合とNodeである場合とで場合分けしている。Nilだった場合はキーは存在しないので単にFalseを返す。Leafだった場合は、保持しているキーのリストから再帰的に探す。Nodeだった場合はそのノードの中にキーがあればOK、なければ適切な部分木の中を再帰的に探索する。
ここでポイントなのがノード内におけるキーの探索方法。キーは昇順に格納されているので、左から順に探索して、xのほうが大きいうちはノード内のキーのリストと部分木のリストの残りの部分(ksとts)に対して再帰的にfindを呼び。そしてxのほうがkより小さくなった時点でkに対応する部分木tに対して再帰的にfindを呼ぶ。感覚的に言えば、xのほうが大きい場合は横に移動して、xのほうが小さい場合は下に移動する。
キーの挿入
キーの挿入操作を実装する。まずはトップレベルの関数insertを定義する。
insert :: (Ord a, Eq a) => Tree a -> a -> Tree a insert t x = if is_full t then insert_non_full (split t) x else insert_non_full t x
まだ定義してない関数がいくつも出てきたけどこれらは順を追って説明する。insertではis_fullを使ってルートノードが full かどうか、つまりキーを (2m-1) 個持っているかどうか(m は B-tree のオーダー)で場合分けする。B-treeの定義より、各ノードは (m-1) 個以上、 (2m-1) 個以下のキーしか持てないのでこの場合分けが必要になる。
ルートノードが full だった場合はノードをsplitして full じゃない状態にしてからinsert_non_fullで実際に挿入する。もともとfull じゃなかった場合はそのままinsert_non_fullで挿入する。Introduction to Algorithms の実装方針はすこし特殊で、あるノードにキーを挿入する場合、挿入対象のノードをまず full じゃない状態にしてから挿入を行う。そうすることによって、ノードの分割処理が親方向に伝搬しないようになる。自分はこの実装方針のほうが理解しやすいと思った。
is_fullは単純で、引数として渡されたTreeが full かどうかを判定する。渡されたTreeがNilなら常にFalseを返す。LeafかNodeだった場合は保持しているキーの数(リストの長さ)が (2m-1) ならTrueを返す。
is_full :: (Ord a, Eq a) => Tree a -> Bool is_full (Nil m) = False is_full (Leaf m ks) | length ks == (2 * m - 1) = True | otherwise = False is_full (Node m ks _) | length ks == (2 * m - 1) = True | otherwise = False
次にsplitを定義しよう。splitが何をしているのかは図を使って説明したほうが良さそうなので、 "Introduction to Algorithms" から図を引用して説明する*2。
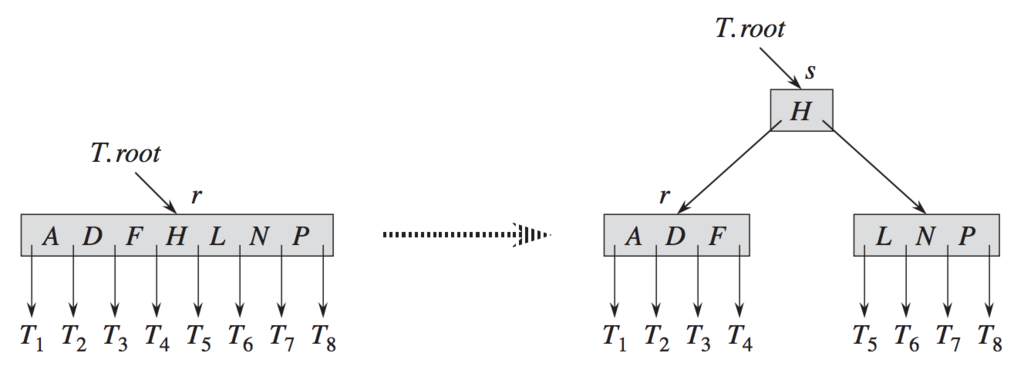
上図を見れば一発でわかると思う。つまり、split関数は full の状態のノードを3つのノードに分割してそれを返す。分割後の部分木のルートノードには分割前のノード内の真ん中のキーを格納する(上図では H)。そして、左の子ノードには分割前のノード内においてキー H より左のキーを、右の子ノードには分割前のノード内においてキー H より右のキーを格納する。
コードは次の通り。上で説明したことをそのまま実装しただけなので特にコードについて説明する点はないと思うけど、分割前のノードに格納されているキーのリストと部分木のリストを前半(first_half)と後半(last_half)に分割して、パターンマッチで新しい木を作り出して返してるだけ。
split :: (Ord a, Eq a) => Tree a -> Tree a split (Leaf m keys) = Node m [k] [Leaf m k1, Leaf m k2] where k1 = first_half keys k:k2 = last_half keys split (Node m keys trees) = Node m [k] [Node m k1 t1, Node m k2 t2] where k1 = first_half keys k:k2 = last_half keys t1 = first_half trees t2 = last_half trees first_half :: [a] -> [a] first_half xs = take (div (length xs) 2) xs last_half :: [a] -> [a] last_half xs = drop (div (length xs) 2) xs
最後に、メインとなるinsert_non_fullを定義しよう。名前の通り、この関数に引数として渡される木は full でないことが保証されている。
ちょっと長いけど、挿入先のノードがNilの場合、Leafの場合、Nodeの場合で場合分けしているだけなので、順を追って見てみよう。
insert_non_full :: (Ord a, Eq a) => Tree a -> a -> Tree a insert_non_full (Nil m) x = Leaf m [x] insert_non_full (Leaf m []) x = Leaf m [x] insert_non_full l@(Leaf m keys@(k:ks)) x | x == k = l | x < k = Leaf m (x:keys) | x > k = Leaf m (k:newKs) where Leaf _ newKs = insert_non_full (Leaf m ks) x insert_non_full (Node m [] (t:ts)) x = if is_full t then insert_non_full (split t) x else Node m [] [(insert_non_full t x)] insert_non_full n@(Node m keys@(k:ks) trees@(t:ts)) x | x == k = n | x < k = if is_full t then insert_non_full (Node m (newK:k:ks) (newT1:newT2:ts)) x else Node m keys ((insert_non_full t x):ts) | x > k = Node m (k:newKs) (t:newTs) where Node _ newKs newTs = insert_non_full (Node m ks ts) x Node _ [newK] [newT1, newT2] = split t
まず、Nilに挿入する場合は単に挿入キーをひとつだけ持ったLeafを返す。これは単純。
次に、Leafに挿入する場合を見てみる。Leafに格納されているキーのリストが空の場合はそこに挿入キーを格納して新しいLeafを返す。キーのリストが空でない場合は、現在注目しているキーkと挿入キーxを比較する。x == kの場合はすでにキーが存在するので、何もせずにそのままlを返す。x < kの場合はxを挿入する場所が見つかったので、xをkeysにつなげて返す。最後にx > kの場合はxを挿入する場所がまだ見つからないので、残りのキーksに対して再帰的にinsert_non_fullをする。そして帰ってきたLeafからパターンマッチでキーのリストnewKsを取り出して、kとくっつけて返す。
最後に、Nodeに挿入する場合について。B-treeではキーの挿入はかならずLeafに対して行うので、Nodeへの挿入は行わず "適切な子部分木" に対して再帰的にinsert_non_fullを呼ぶことになる。またinsert_non_fullを呼ぶ前には、対象となる部分木が full であるかどうかを必ずチェックして、 full であるなら split してから insert_non_fullをする。
"適切な子部分木" を見つける部分はLeafのときとほとんど同じなんだけど、x == kのときはすでにキーが存在するので何もせず、x < kのときは "適切な子部分木" が見つかったのでそこに再帰的にinsert_non_fullをし、x > kのときはまだ "適切な子部分木" が見つからないので残りのキーの中からの探索を続ける。
テスト
実装できたので簡単にテストする。オーダーm=2のB-treeを作る。まず適当に作ったキーのリストに対してfoldlで順にinsertして木を得る。pretty print はサボったので見づらいんだけど、ちゃんとB-treeの定義に従った深さ3の木ができているのが分かる。挿入したキーを探索すると全て見つかるし、挿入していないキーを探索するともちろん見つからない。うまく動いてるっぽい。
*Main> :l btree [1 of 1] Compiling Main ( btree.hs, interpreted ) Ok, one module loaded. *Main> keys = [432,463,7,453,1,52,7,8,6,35,756,987,4454,765] *Main> t = foldl insert (Nil 2) keys *Main> t Node 2 [432] [Node 2 [7] [Leaf 2 [1,6],Leaf 2 [8,35,52]],Node 2 [463,987] [Leaf 2 [453],Leaf 2 [756,765],Leaf 2 [4454]]] *Main> map (find t) keys [True,True,True,True,True,True,True,True,True,True,True,True,True,True] *Main> find t 9999999 False
キーの削除
次回!
2017年まとめ
研究者からエンジニアに転職
個人的にはかなり悩んだんだけど、結局これといった "かっこいい理由" みたいなものも特になくて、研究者だけじゃなくていろいろやってみたかったからという感じで転職してみた。研究者もエンジニアもどっちも楽しい!
論文が3本出た
論文がIJCAIでファースト2本、CIKMで学生さんファーストのポスターが1本出た。とりあえず自分の研究者としての仕事は一旦ここまで。また機会を見て戻ってきたい。
When Does Label Propagation Fail? A View from a Network Generative Model @ IJCAI2017
ラベル伝搬法がネットワーク生成モデルの一つである確率的ブロックモデルと理論的につながっていることを示し、ネットワーク生成モデルの見地からラベル伝搬法の性質を解析する論文。
www.slideshare.net
Tensor Decomposition with Missing Indices @ IJCAI2017
テンソル分解は観測データの "値" が欠損している場合でも柔軟に対応できるんだけど、観測データの "インデックス" が欠損している場合は対応できなかった。それを可能にした論文。
www.slideshare.net
Collecting Non-Geotagged Local Tweets via Bandit Algorithms @ CIKM 2017
学生さんファーストの論文。特定の地域から発信されたツイートをバンディットアルゴリズムを用いて効率的に集める手法を提案。シンプルな手法だけどアイデアが面白いということで採択されたのかな。
講演とか
今年は機会を頂いて3つ講演した。どれもそうそうたるメンバーに混じっての講演だったので粗相のないように頑張った。
ERATO感謝祭 Season IV
言わずと知れた河原林ERATO関連の研究成果が二日間でものすごいたくさん聞けるものすごい会。自分はERATOのメンバーではないんだけど、共著者の林さんがERATOのメンバーだったということで感謝祭で話す機会を頂いた。
資料
ビッグデータ基盤勉強会
筑波大学の川島先生、大阪大学の鬼塚先生、トレジャーデータの油井さんが運営している勉強会。怖い。既に何回か参加させて頂いていたが、今回は話す機会を頂いた。自分が話した内容は機械学習関連だったので、全然基盤とかシステムは関係ないんだけど、今回の勉強会は機械学習的なことを話している人も結構いたので、OKだったっぽい。
www.slideshare.net
情報システム特別講義D@筑波大学
大学の講義なので情報はあまり外に出ていないけど、そうそうたる方々が外部講師となって毎年?行われる講義。そんななか恐縮ながら自分も講師として参加させていただいた。講義資料は一応大学の講義なので非公開。上のビッグデータ基盤勉強会の内容をかなり基礎的なところから時間をかけて講義してみた。
書いたブログ記事
ノンパラ
佐藤先生のあの本読んでノンパラ1ミリ分かった気分になったので書いた。
トピックモデル
青いトピックモデル本を読んでトピックモデル1ミリ分かった気分になったので書いた。
- Joint Topic Modelを実装した
- Correspondence Topic Model の導出と実装
- Noisy Correspondence Topic Model の導出と実装
- Author Topic Model の導出と実装
Edward
Edward触ってみて最初は「これいいじゃん」という気持ちになって、記事書いたんだけど、ちょっと込み入ったことしようとすると辛くなってきて辛かった。
その他
学振PDでカーネギーメロン大学に留学
研究留学 Advent Calender 2017 の19日目です。特にこれといったテーマも思いつかなかったので、エッセイ的に書きます。
テンプレ
- いついったか:2014年4月から2015年3月
- どこに行ったか:カーネギーメロン大学の Christos Faloutsos 教授のところ(ペンシルベニア州ピッツバーグ)
- 何をやったか:ソーシャルデータとかグラフデータに対するデータマイニングの研究
- どうやって行ったか:出身研究室の教授の紹介(つまりコネ)
行くまで(だけ)が辛かった
Dとった直後に行くことが決まっていたので、博論を書きつつビザ取得とか家探しとかの留学準備をしなくちゃいけなくて、さらにちょうどその時期に結婚したのでその辺の諸々も含めすべて同時にこなさなきゃいけなくてそれはそれは辛かった。人生の節目となるイベントを2つ以上同時にこなすのはやめたほうが良い!
ピッツバーグで暮らす
ピッツバーグで暮らす人はまずは何も言わずにピッツバーグ便利帳を見ましょう。ピッツバーグに滞在する人なら誰しもがお世話になるはず(お世話になりました)。ピッツバーグにはほとんど遊ぶところは無いんだけど、暮らすにはとても良いと思う。バスがかなりしっかり通っているので、車を買わなくても全然生活できる。実際自分は結局車は買わなかった。スーパーも多いし、飲食店もそこそこある。あとは、周辺(?)にナイアガラの滝とか、ワシントンとか、ニューヨークとかあるので、そのへんに遊びに行く人は多い。以前役に立つんだか立たないんだかよくわからない TIPS をここに書いたので参考になれば。
学振PDの給料だとギリギリ!
言わずもがな、海外で外食するととても高い。ピッツバーグは家賃は安かった(1 bedroomで1000ドルくらい)けど、それでも高い。それに自分が留学したときの2014-2015年は1ドル125円くらいしたので、いまと比べると給料が10%くらい目減りしていることになる。さらに、自分は奥さんに仕事をやめてもらって夫婦で行ったので、二人分の生活費を賄うのはギリギリだった。
研究のサイクルを短く多く!
留学に行く前に自分は留学中に何に専念したいかを考えてみたんだけど、せっかく有名研究室に行くんだから、知識を得てくるというよりは、研究の方法論みたいのを学んだほうがいいんじゃないかと思ってそうしてみた。どうしたかというと、
- そこまで良いアイデアだと思わなくても、なんでもかんでも教授に提案して、議論させてもらう。
- Faloutsos 教授は研究テーマ作りの天才(というか神)なので、僕がもっていったそこまで良くないアイデアでも議論を通じて研究テーマまで昇華させてくれた。
- 研究テーマが出来上がったので、毎週毎週教授とミーティングすることができる*1。教授と頻繁に話すことで、超一流研究者の研究の進め方みたいなものが見えてくる。
- ある程度議論が進んだらこの内容で論文を書きたいと言って、書かせてもらう。Faloutsos 教授は大枠の添削はしてくれたので、論文の書き方がかなり学べた。
- 論文が書き終わったらまた1へ。
これが大当たりで、本当にいろんなことを学ぶことができた。とくに論文の書き方を学べたことはその後の自分の研究者としての価値を大いに高めてくれたと思う(価値が高いとは言っていない)。実際に論文の採択率はかなり上がったし、査読結果にも "well written" と書かれることが多くなった。Faloutsos 教授から学んだ論文の書き方は昔ここに書いた。
なんか生活にゆとりがある気がした
日本にいたときと比べて、生活にかなりゆとりがある気がした。日本にいたとき以上に研究に時間を割いていたのに、1年の間にいろんなところに旅行に行ったり、週末はちょっと遠出で遊びに行ったり、夏は(アパートについてる)プールで毎日泳いだりしてた。理由はよくわからないんだけど、たぶんアメリカは一日が24時間以上あるんだと思う。いまの生活にゆとりがないなぁとか思う人はいっぺんガラッと環境を変えてみるのをオススメします。
ともだちを作ろう
soramichiさんも書いていたけど、留学生活において友達がいるのといないのでは天と地の差があると思う。自分はこの留学中にブラジル人のともだちができてよく一緒に遊びに行った。単純に楽しかったし、英語も(少し)上達するし、共同研究もできた*2。同じ分野なので、その後の国際会議でも会って一緒に観光したりできた。留学中の友達ってなんとなく特別な気がしていて、日本とブラジルだし国際会議を除いて全く会っていないんだけど、今後も連絡を取り合ったりしていくと思う。
何より刺激になる
とにかく周りのレベルが高い。高すぎた。PhD student になりたての学生がすでにもう KDD とか WWW の論文を数本持っていたりする*3。そんな感じの学生たちと同じ環境にいながら、たまに議論をしながら研究を進めていると思うだけで、自分がいかにちっぽけかを痛感してより一層がんばろうと思えた。月並みだとは思うけど、留学で得た効能としてはこれが一番だったんじゃないだろうか。
Stochastic Block Model を Edward で実装する
前回の記事で Edward を使ってみたらすごく良かったので、もう一回遊んでみる。今回はグラフクラスタリングによく使われる Stochastic Block Model (SBM) を実装する。
前回の記事はこれ。
ちなみにプルリク送ったらマージされたので、コードはリポジトリの edward/examples/stochastic_block_model.py にある。
Stochastic Block Model
Stochastic Block Model (SBM) はグラフの確率的生成モデルの一つ。グラフの確率的生成モデルと言うと、有名どころでは Erdos-Renyi model とか Barabasi-Albert model とかあるけど、そういうやつ。
SBM がどういうモデルなのか、すごく簡単に説明する。ものすごくざっくり言うと、SBM は以下の2つの仮定を置いたモデルだといえる。
- すべてのノードは、K 個あるクラスタのうち(必ず)どれか一つに属している。
- あるノード i とノード j の間にエッジが存在する確率は、i と j がどのクラスタに属しているか のみ によって定まる。
めちゃくちゃシンプルなモデルなんだけど、これが結構注目されていて、いろいろ理論的な解析がされていたり、グラフクラスタリングに応用されていたり、拡張モデルがいろいろ提案されていたりする。
例を使って説明してみよう。例えば、グラフ上に3つのクラスタがあり、それぞれのクラスタ間には以下の確率でエッジが張られるということがわかっているとしよう。
$$ \left( \begin{array}{ccc} 0.9 & 0.2 & 0.2 \\ 0.1 & 0.3 & 0.7 \\ 0.1 & 0.8 & 0.1 \end{array} \right) $$
これは例えば、(2,3)要素を見ると、2番目のクラスタに属すノードから3番目のクラスタに属すノードへエッジが張られる確率は 0.7 であるということを表している。上にも書いたように、SBMではクラスタ2に属すどんなノードからも、クラスタ3に属すノードへエッジが張られる確率は等しく 0.7 であるという仮定を置く。 ここが SBM で最も重要。グラフ上のノードはいろいろな性質(例えばTwitterユーザなら性別、年齢、趣味、居住地などなど)を持つわけだけど、それらはすべて無視して、そのノードがどのクラスタに属すかのみによって張られるエッジが決まる。ここが SBM がシンプルたる所以。
さて、実際の生成過程を見ていこう。ノード数は N 、クラスタ数は K とする。
まず、1 から N の i について、クラスタ割りあて を以下のように生成する。
$$ z_{i} \sim Categorical(\gamma) $$
ここで、 は K 次元のベクトルで、各クラスタにどれくらいの割合でノードが所属するかを表すパラメータ。Categorical 分布のパラメータなので、当然
となっている必要がある。
は 1 から K の整数で、例えば
ならノード i がクラスタ2に属すことを表す。
つぎに、1 から N の i と j のすべての組み合わせについて、隣接行列 の要素を以下のように生成する。
$$ X_{ij} \sim Bernoulli(\Pi_{z_{i}z_{j}}) $$
は上に書いたような K x K 行列で、各クラスタ間にどれくらいの確率でエッジが存在するかを表すパラメータ。Bernoulli 分布のパラメータなので、
の要素はすべて0以上1以下である必要がある。
生成過程は以上。とてもシンプル。2つのパラメータ と
を決めてやればなんらかの隣接行列
が確率的に生成される。また、それと同時に各ノードがどのクラスタに属すかを表す
も生成される。 つまり、ノードのクラスタリングが得られる。
ちなみに、簡単のため上では と
の生成過程しか書かなかったけど、多くの場合、
と
に次のように事前分布を入れる。
$$ \gamma \sim Dirichlet(\alpha) $$
1 から K のすべての k, l の組み合わせについて、
$$ \Pi_{kl} \sim Beta(a, b) $$
ここで、 は Dirichlet 分布のパラメータで、
と
は Beta 分布のパラメータ。
モデルが定義できたらパラメータを推定したくなるのが世の常なわけで、それを Edward つかってやっちゃいましょうってのが今回の記事の趣旨。普通は VB やら MCMC やらを頑張って導出して頑張って実装するんだけど、Edward を使うとその辺をすっ飛ばして楽に実装できる。ちなみに、MCMCの導出は毎度おなじみ『関係データ学習』に詳しく載ってるので参考にしてもらえるといいとおもう。

- 作者: 石黒勝彦,林浩平
- 出版社/メーカー: 講談社
- 発売日: 2016/12/07
- メディア: 単行本(ソフトカバー)
- この商品を含むブログ (1件) を見る
Edward で実装
さて、いよいよ Edward で実装する。Edward そのものの使い方については本家チュートリアルをみてもらうなり、前回の記事をみてもらうなりしてほしい。
まず必要なものをインポートする。適当に乱数シードも決めておく。
import edward as ed import numpy as np import tensorflow as tf from sklearn.metrics.cluster import adjusted_rand_score from edward.models import Bernoulli, Multinomial, Beta, Dirichlet, PointMass ed.set_seed(42)
そんで次にデータを用意する。edward/examples/data/以下に必要なデータが置いてあるので、それを読んでいる。この example コードではかの有名な Zachary’s karate club のデータを使う。
def build_dataset(label_filepath, graph_filepath): Z = np.loadtxt(label_filepath, dtype=np.int) N = Z.shape[0] X = np.zeros((N, N)) for line in open(graph_filepath, 'r'): src, dst = map(int, line.strip().split(' ')) X[src, dst] = 1 return X, Z # DATA label_filepath = 'data/karate_labels.txt' graph_filepath = 'data/karate_edgelist.txt' X_data, Z_true = build_dataset(label_filepath, graph_filepath) N = X_data.shape[0] # number of vertices K = 2 # number of clusters
モデルを定義する。上に書いた生成過程をそのままコードにしたような感じで、非常に書きやすい。 と
にも事前分布を入れている。
tf.matmulは行列積で、tf.transposeは転置をしている。
# MODEL gamma = Dirichlet(concentration=tf.ones([K])) Pi = Beta(concentration0=tf.ones([K, K]), concentration1=tf.ones([K, K])) Z = Multinomial(total_count=1., probs=gamma, sample_shape=N) X = Bernoulli(probs=tf.matmul(Z, tf.matmul(Pi, tf.transpose(Z))))
モデルが定義できたらいよいよパラメータを推定する。今回は簡単に MAP を EM algorithm で推定する。PointMassはそのパラメータを点推定するよということを宣言していると思っていい。
# INFERENCE (EM algorithm) qgamma = PointMass(params=tf.nn.softmax(tf.Variable(tf.random_normal([K])))) qPi = PointMass(params=tf.nn.sigmoid(tf.Variable(tf.random_normal([K, K])))) qZ = PointMass(params=tf.nn.softmax(tf.Variable(tf.random_normal([N, K])))) inference = ed.MAP({gamma: qgamma, Pi: qPi, Z: qZ}, data={X: X_data}) n_iter = 100 inference.initialize(n_iter=n_iter) tf.global_variables_initializer().run() for _ in range(inference.n_iter): info_dict = inference.update() inference.print_progress(info_dict) inference.finalize()
パラメータが推定できたので、最後にモデルを評価する。評価指標には Adjusted Rand Index (ARI) を使う。
# CRITICISM Z_pred = qZ.mean().eval().argmax(axis=1) print("Result (label filp can happen):") print("Predicted") print(Z_pred) print("True") print(Z_true) print("Adjusted Rand Index =", adjusted_rand_score(Z_pred, Z_true))
結果は以下のようになる。クラスタリング結果と正解が完全に一致していれば ARI は 1 になるんだけど、一つ間違っていたので ARI = 0.88 になった。まぁそれでも SBM はこのデータをかなり正しくクラスタリングできたと言えると思う。
Result (label filp can happen): Predicted [0 0 0 0 0 0 0 0 1 1 0 0 0 0 1 1 0 0 1 0 1 0 1 1 1 1 1 1 1 1 1 1 1 1] True [0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 1 0 1 0 1 1 1 1 1 1 1 1 1 1 1 1] Adjusted Rand Index = 0.882257541356
まとめ
やっぱ Edward いいわ。