でかいチーズをベーグルする

でかいチーズはベーグルすべきです。

Tucker分解の導出と実装

CP分解の次はTucker分解を導出して実装する。丁寧にTucker分解の導出を説明してる文献（Web含め）が全然なかったので、自分で書く。CP分解についてはある程度知ってる前提とする。CP分解についてはこちらから。

yamaguchiyuto.hatenablog.com

まとめ

  • Tucker分解とは
  • ALSでTucker分解の更新式の導出
  • PythonでTucker分解を実装
  • 人工データを使って実験

Tucker分解とは

Tucker分解は、テンソルを１つのテンソル（コアテンソルと呼ぶ）と、それぞれのモードに対して一つずつの行列に分解する。

f:id:yamaguchiyuto:20161127144753p:plain

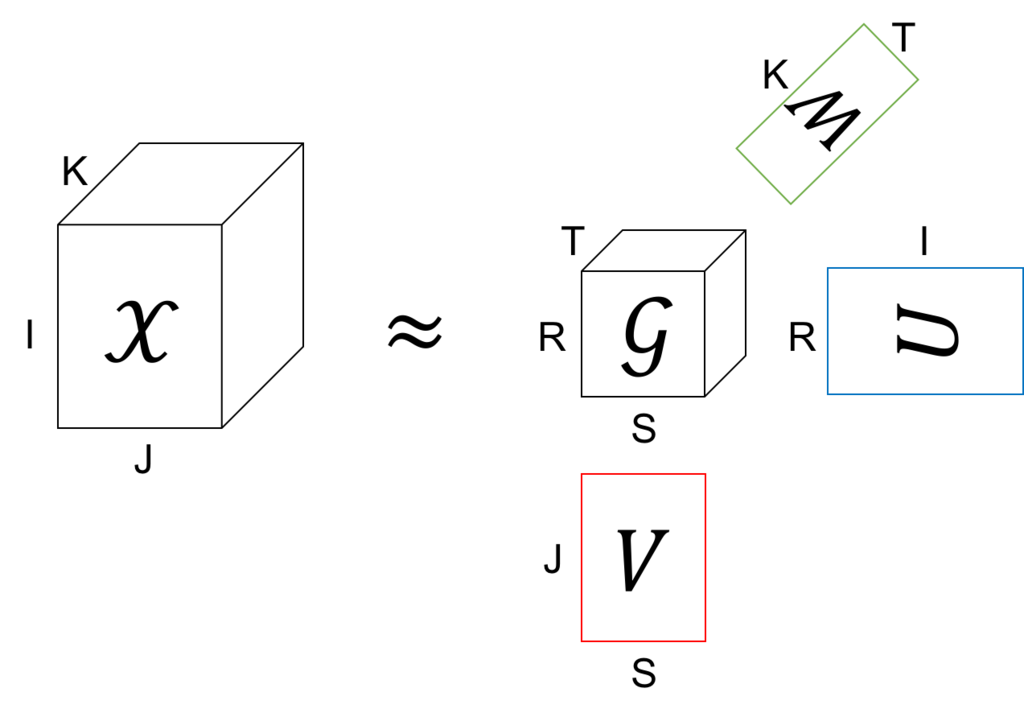
上の図の例では、もとのテンソルのサイズは IxJxK だけど、これをコアテンソルのサイズの RxSxT (R<=I, S<=J, T<=K) まで小さくしている。また、あとで説明するけど、行列 U、V、W は全て直行行列となるように分解する。このコアテンソル {\mathcal{G}} と３つの直交行列を使ってもとのテンソル {\mathcal{X}} を近似する。

これを式で書くと、

{ x_{ijk} \simeq \sum_{rst} g_{rst} u_{ir} v_{js} w_{kt} }

という分解をしていることになる。

この分解が何かに似ていると思った人はお目が高い。実は、コアテンソルが対角要素が全部1の対角テンソルのとき、Tucker分解はCP分解と等しくなる。つまり、CP分解はモデル的にはTucker分解の特殊ケースということになる。

ALSでTucker分解の更新式の導出

上で説明したように、Tucker分解ではテンソル {\mathcal{X}} を１つのコアテンソル {G} と、（テンソルが３階の場合は）３つの直交行列 {U}、{V}、{W}に分解する。分解の方針はCP分解のときと同じで、ALS (Alternating Least Square) で行く。

さて、以下のコスト関数を最小にすることを考える。

{ L = \frac{1}{2} \sum_{ijk} \left(x_{ijk} - \sum_{rst} g_{rst} u_{ir} v_{js} w_{kt} \right)^{2} }

これはただ単にテンソル {X} の全要素について近似誤差の和の二乗を取っているだけ。ただし、問題を簡単にするために {U}、{V}、{W} は直交行列であるとする。

L を {g_{abc}} で微分すると

{ \frac{\partial L}{\partial g_{abc}} = - \sum_{ijk} \left(x_{ijk} - \sum_{rst}g_{rst}u_{ir}v_{js}w_{kt}\right)\left(u_{ia}v_{jb}w_{kc}\right) }

{ = - \sum_{ijk}x_{ijk}u_{ia}v_{jb}w_{kc} +\sum_{ijk}\sum_{rst}g_{rst}u_{ir}v_{js}w_{kt}u_{ia}v_{jb}w_{kc} }

{ = - \sum_{ijk}x_{ijk}u_{ia}v_{jb}w_{kc} +\sum_{rst}g_{rst}\sum_{i}u_{ir}u_{ia}\sum_{j}v_{js}v_{jb}\sum_{k}w_{kt}w_{kc} }

ここで、{U} は直交行列だから、{r\neq a} のとき {\sum_{i} u_{ir} u_{ia} = 0}、また {r = a} のとき、{\sum_{i} u_{ir} u_{ia} = 1} となる。よって、

{ = - \sum_{ijk}x_{ijk}u_{ia}v_{jb}w_{kc} + g_{abc} }

これを 0 と置いて {g_{abc}} について解くと、

{ g_{abc} = \sum_{ijk}x_{ijk}u_{ia}v_{jb}w_{kc} }

となる。これを★とする。

★を L に代入するが、その前にまず L をちょっと変形すると

{ L = \frac{1}{2} \sum_{ijk} \left(x_{ijk} - \sum_{rst} g_{rst} u_{ir} v_{js} w_{kt} \right)^{2} }

{ = \frac{1}{2} \sum_{ijk} \left(x_{ijk}^{2} - 2x_{ijk}\sum_{rst} g_{rst} u_{ir} v_{js} w_{kt} + \left(\sum_{rst}g_{rst}u_{ir}v_{js}w_{kt}\right)^{2}\right) }

{ = \frac{1}{2} \sum_{ijk} x_{ijk}^{2} - \sum_{ijk} x_{ijk}\sum_{rst} g_{rst} u_{ir} v_{js} w_{kt} + \frac{1}{2} \sum_{ijk} \left(\sum_{rst}g_{rst}u_{ir}v_{js}w_{kt}\right)^{2} }

ここで、第二項を変形して★を代入すると、

{ \sum_{ijk} x_{ijk}\sum_{rst} g_{rst} u_{ir} v_{js} w_{kt} = \sum_{rst} g_{rst} \sum_{ijk} x_{ijk} u_{ir} v_{js} w_{kt} }

{ = \sum_{rst} g_{rst} g_{rst} = \sum_{rst} g_{rst}^{2} }

また第三項に★を代入すると、

{ \sum_{ijk} \left(\sum_{rst}g_{rst}u_{ir}v_{js}w_{kt}\right)^{2} = \sum_{ijk} \left(\sum_{rst}\sum_{abc}x_{abc}u_{ar}v_{bs}w_{ct}u_{ir}v_{js}w_{kt}\right)^{2} }

{ = \sum_{ijk} \left(\sum_{abc}x_{abc}\sum_{r}u_{ar}u_{ir}\sum_{s}v_{bs}v_{js}\sum_{t}w_{ct}w_{kt}\right)^{2} }

ここでまた {U} が直交行列なので、{a = i} かつ {b = j} かつ {c = k} のときの項のみが残って、

{ = \sum_{ijk} x_{ijk}^{2} }

となる。

まとめると、Lは以下のように書ける。

{ L = \sum_{ijk} x_{ijk}^{2} - \sum_{rst} g_{rst}^{2} }

結局、L を最小化するという問題は、{U}、{V}、{W}が直行という制約のもとで

{\sum_{rst} g_{rst}^{2} = \sum_{rst}\left(\sum_{ijk}x_{ijk} u_{ir}v_{js}w_{kt}\right)^{2} }

を最大化するという問題に帰着した（やっとスタート地点に立った・・・）。これを L' と置こう。

さて、ALSなので、{V} と {W} を固定して、L' を最大化する {U} を求める。

今後の見通しを良くするために L' をちょっと変形する、

{ L' = \sum_{rst}\left(\sum_{ijk}x_{ijk} u_{ir}v_{js}w_{kt}\right)^{2} }

{ = \sum_{rst}\left(\sum_{i} u_{ir} \sum_{jk} x_{ijk}v_{js}w_{kt}\right)^{2} }

ここで {\sum_{jk} x_{ijk}v_{js}w_{kt} = x^{VW}_{ist}} と置くと、

{ = \sum_{rst}\left(\sum_{i} u_{ir} x^{VW}_{ist}\right)^{2} }

また、添字 s と t をまとめて q と書くと*1、

{ = \sum_{rq}\left(\sum_{i} u_{ir} x^{VW}_{iq}\right)^{2} = \sum_{rq}\left(u_{r}^{T} x^{VW}_{q}\right)^{2} }

ここで、{x^{VW}_{q} = (x^{VW}_{1q}, \cdots, x^{VW}_{Iq})^{T}}、{u_{r} = (u_{1r}, \cdots, u_{Ir})^{T}} とした。すべての {u_{r}} は独立に考えられるから、ある {u_{r}} について {u_{r}^{T}u_{r}=1} の制約のもとで L' を最大化する。

{ L'(r) = \sum_{q}\left(u_{r}^{T} x^{VW}_{q}\right)^{2} - \lambda_{r} (u_{r}^{T}u_{r}-1) }

とおいて、{u_{r}} で微分すると、

{ \frac{\partial L'(r)}{\partial u_{r}} = 2\sum_{q}\left(u_{r}^{T} x^{VW}_{q}\right)x^{VW}_{q} - 2\lambda_{r} u_{r} }

{ = 2 \sum_{q}\left(x^{VW}_{q} (x^{VW}_{q})^{T}\right)u_{r} - 2\lambda_{r} u_{r} }

{X^{VW} = (x^{VW}_{1}, \cdots, x^{VW}_{Q})} と置くと、

{ = 2X^{VW}(X^{VW})^{T}u_{r} - 2\lambda_{r} u_{r} }

これを 0 と置くと、

{ X^{VW}(X^{VW})^{T}u_{r} = \lambda_{r} u_{r} }

つまり、{u_{r}} は 行列 {X^{VW}(X^{VW})^{T}} の固有ベクトル、また行列 {X^{VW}} の左特異ベクトルということになる。

この {u_{r}} を全ての r について互いに直交するように求めれば良いから、結局行列 {X^{VW}} を特異値分解して得られる左特異ベクトルが答えとなる。

長かった・・・。

{V} と {W} についても同様に求まる。まとめると、

  1. {U^{(0)}}、{V^{(0)}}、{W^{(0)}} を適当に初期化する
  2. {k \leftarrow 0}
  3. {X^{V^{(k)}W^{(k)}}} を 特異値分解し、左特異ベクトルを {U^{(k+1)}} とする
  4. {X^{W^{(k)}U^{(k+1)}}} を 特異値分解し、左特異ベクトルを {V^{(k+1)}} とする
  5. {X^{U^{(k+1)}V^{(k+1)}}} を 特異値分解し、左特異ベクトルを {W^{(k+1)}} とする
  6. {k \leftarrow k+1}
  7. 収束するまで 2-6 を繰り返す。
  8. ★により {\mathcal{G}} を求める。

実装

scipy.sparse は疎テンソルを扱えないので、データテンソルは X[(indices)]=value という辞書で与えた。indicesはインデックスが入ったタプル。

gist74f1026096be91ba0a147eeaa540326c

実験

平均0、標準偏差1の正規分布でコアテンソル {\mathcal{G}} と直交行列 U、V、W を初期化し、データテンソル {\mathcal{X}} を作って、平均0、標準偏差0.1の正規ノイズを加えた。

Tucker分解が真のコアテンソル {\mathcal{G}} と直交行列 U、V、W を復元できるか試した。

max_iter=5 としたけど、一回で（ほぼ）収束した。収束するまで特異値分解し続けるのがHOOI、一回だけ特異値分解するのがHOSVDと呼ばれてるけど、この例ではHOSVDで十分っぽい。

学習した後に残差（の平均）を見てみたけど十分小さいのでOK。

gist86035070f286f595f3f1078ed2002e3a

*1:q = s*T + t とすればよい

クロネッカー積とvec作用素とRoth's column lemma

クロネッカー積とvec作用素は見た目簡単なんだけど、各要素のインデックスを書き下すと頭の中こんがらがってわけわからなくなるから一旦整理した。インデックスに関する記事ってほとんどないね。あとそれに関連して Roth's column lemma っていうのが便利なのでちょっと紹介する。

まとめ

クロネッカー積とは

クロネッカー積 - Wikipedia

下の式を見ればひと目で分かるけど、 IxJ 行列 {A} と KxL 行列 {B} から IKxJL 行列を作る。

{ A \otimes B = \left( \begin{array}{ccc} a_{11} B & \cdots & a_{1J} B \\ \vdots & \ddots & \vdots \\ a_{I1} B & \cdots & a_{IJ} B \end{array} \right) }

Wikipediaの例を見ると分かりやすい。

https://wikimedia.org/api/rest_v1/media/math/render/svg/130f0defabfa409a56ff89937d40f1656fcb108f

クロネッカー積のインデックス

クロネッカー積の定義は一目見ればすぐ分かるのに、各要素の定義を見ると途端にめんどくさくなる。

{ \left[A \otimes B\right]_{(i-1)K+k,(j-1)L+l} = a_{ij}b_{kl} }

行のインデックスを見ると、K進数みたいになってるのが分かる。 {A} の行のインデックスが1つ増えるためには、{B} の行のインデックスを一回ずつ辿らなきゃいけないって考えるとそうなることが分かる。列についても同じ。

実験

上式のインデキシングが本当に合ってるのか numpy.kron を使って確かめる。

gist6cf39c77df3bf44fe6ed5aaf98c343cc

vec作用素

vec作用素 - Wikipedia

vec作用素は、以下のように IxJ 行列 {A} の列ベクトルを全て一列に並べて1つの大きな IJ 次元列ベクトルを作る。

{ vec(A) = \left( \begin{array}{c} a_{1} \\ a_{2} \\ \vdots \\ a_{J} \end{array} \right) }

例えば、以下のようになる

{ vec\left( \begin{array}{ccc} 1 & 3 & 2 \\ 0 & 7 & 4 \end{array} \right) = \left( \begin{array}{c} 1 \\ 0 \\ 3 \\ 7 \\ 2 \\ 4 \end{array} \right) }

vec作用素のインデックス

こっちはクロネッカー積よりは簡単。

{ \left[vec(A)\right]_{(i-1)J+j} = a_{ij} }

クロネッカー積のときと同じで、J進数みたいになってる。各列ベクトルがJ次元なので、{a_{ij}} の {i} が増えるためには {j} を全部辿らなきゃならない。

Roth's column lemma

これが成り立つ。

{ vec(XYZ) = (Z^{T} \otimes X)vec(Y) }

証明

{X} をIxJ行列、{Y} をJxK行列、{Z} をKxL行列とし、

{W = XYZ}

と置く。{W} は IxL 行列。

{W} の各要素は（とうぜん）以下のように書ける。

{ w_{il} = \sum_{pq} x_{ip}y_{pq}z_{ql} }

クロネッカー積の要素を考えると

{ \left[Z^{T} \otimes X\right]_{(l-1)I+i,(k-1)J+j} = z_{kl}x_{ij} }

vec作用素の要素を考えると

{ \left[vec(Y)\right]_{(j-1)K+k} = y_{jk} }

{ \left[vec(W)\right]_{(i-1)L+l} = w_{il} }

なので、以下の行列ベクトル積の要素を考えると、

{ \left[(Z^{T} \otimes X)vec(Y)\right]_{(i-1)L+l} }

{ = \sum_{pq} \left[Z^{T} \otimes X\right]_{(l-1)I+i,(q-1)J+p} \left[vec(Y)\right]_{(p-1)J+q} }

{ = \sum_{pq}z_{ql} x_{ip} y_{pq} }

{ = \sum_{pq}x_{ip} y_{pq}z_{ql} }

{ = w_{il} = \left[vec(W)\right]_{(i-1)L+l} }

{W=XYZ} だから、証明完了。

Alternating Least Square (ALS) でCP分解

テンソル分解の基本中の基本のCP分解を導出して実装した。最適化の方法は色々あるらしいけど多分いちばんよく使われる Alternating Least Square (ALS) を使った。ちなみにここでテンソルって呼んでるのはただの多次元配列のこと。

まとめ

  • CP分解とは
  • AlSによるCP分解の更新式を導出
  • ALSによるCP分解をpythonで実装
  • 人工データを使って実験

CP分解とは

CP分解が何かを知るためには、まず Matrix factorization (MF) について知ると良い。

MFでは、N x M 行列 X を以下のように分解する

{ X \simeq P Q^{T} }

ここで、{P}は N x R 行列で、{Q}は M x R 行列。この分解を要素ごとに書くとこうなる

{ x_{ij} \simeq \sum_{r} p_{ir} q_{jr} = p_{i}^{T}q_{j} }

つまり要素 {x_{ij}} を なんかよくわからない{r}次元のベクトル {p_{i}}と{q_{j}}の内積で表現することにしましょうと言っているわけ。

じゃあこの {p_{i}} と {q_{j}} っていうベクトルたちをどうやって求めるかという話になるわけだけど、それはこの辺に良い説明があるので説明しない。

Matrix Factorization: A Simple Tutorial and Implementation in Python @ quuxlabs

Matrix Factorizationとは - Qiita

ここまでわかるとCP分解が何なのかはすぐに理解できる。3階の I x J x K テンソル {\mathcal{X}} のCP分解は要素ごとに書くと以下のようになる

{ x_{ijk} \simeq \sum_{r} u_{ir} v_{jr} w_{kr} }

これはMFとほぼ同じで、右辺が3つの積になっただけ。簡単簡単。ほんとにこれだけ。

この記事では、この {u_{i}} と {v_{j}} と {w_{k}} をどう求めるかを説明する。以下では、{u_{i}} と {v_{j}} と {w_{k}}をまとめて

{ U^{T} = (u_{1}, \cdots, u_{I}), V^{T} = (v_{1}, \cdots, v_{J}), W^{T} = (w_{1}, \cdots, w_{K}) }

と表記する。

ちなみにCP分解はCanonical Polyadic分解の略だけど、ほかにもいろんな呼び名があって、例えばPARAFAC（Parallel Factor Analysis）とか、CANDECOMP（Canonical Decomposition）とか。なぜか知らないけどいろいろある。ここではとりあえずCP分解に統一する。

CP分解のALSによる更新式の導出

上で軽く説明したように、CP分解では3階の I x J x K テンソル {\mathcal{X}} *1 を3つの行列 {U}、{V}、{W} （潜在変数行列と呼ぶ）に分解するわけだけど、ALS は簡単に言うと「他の2つを固定して、1つの潜在変数を最小二乗法で推定する」という方法。それを繰り返して更新していく。だから "Alternating" Least Square と呼ばれる。

ではまず {U} をどう推定するかを考える。

最小二乗なので、コスト関数を以下で定義する

{ L = \frac{1}{2} \sum_{ijk} \left(x_{ijk} - \sum_r u_{ir}v_{jr}w_{kr}\right)^{2} }

ただ単に全要素の差の二乗を取っているだけ。これを今後の見通しが良くなるように書き換える

{ L = \frac{1}{2} \sum_{ijk} \left(x_{ijk} - u_{i}^{T}(v_{j} \circ w_{k}) \right)^{2} }

{\circ} はベクトルの要素積（アダマール積という）。

んで、これを最小化する{U}を求めたいので、{u_{i}}で微分する

{ \frac{\partial L}{\partial u_{i}} = - \sum_{jk} \left(x_{ijk} - u_{i}^{T}(v_{j} \circ w_{k})\right)\left(v_{j} \circ w_{k}\right) }

{ = - \sum_{jk} x_{ijk}(v_{j} \circ w_{k}) + \sum_{jk}u_{i}^{T}(v_{j} \circ w_{k})(v_{j} \circ w_{k}) }

{ = - \sum_{jk} x_{ijk}(v_{j} \circ w_{k}) + \sum_{jk}(v_{j} \circ w_{k})(v_{j} \circ w_{k})^{T}u_{i} }

{ = - \sum_{jk} x_{ijk}(v_{j} \circ w_{k}) + (V^{T}V \circ W^{T}W)u_{i} }

ここで、

{ \bar{x}^{vw}_{i} = \sum_{jk}x_{ijk}\left(v_{j} \circ w_{k}\right) }

というベクトルを定義すると、以下のように書ける

{ \frac{\partial L}{\partial u_{i}} = - \bar{x}^{vw}_{i} + (V^{T}V \circ W^{T}W)u_{i} }

これを0と置いて解くと、

{ u_{i} = (V^{T}V \circ W^{T}W)^{-1}\bar{x}^{vw}_{i} }

となる。また、{(\bar{X}^{wv})^{T} = (\bar{x}^{wv}_{1}, \cdots, \bar{x}^{wv}_{I})} と置いて行列で書くと、

{ U = \bar{X}^{vw}\left(V^{T}V \circ W^{T}W\right)^{-1} }

となり、これで{U}が求まった。

同様に、{V} と {W} もついても以下のように書ける

{ V = \bar{X}^{wu}\left(W^{T}W \circ U^{T}U\right)^{-1} }

{ W = \bar{X}^{uv}\left(U^{T}U \circ V^{T}V\right)^{-1} }

このように、ALSでは2つの潜在変数行列を固定して、1つの潜在変数行列を更新するということを繰り返す。まとめると、

  1. {U_{(0)}}、{V_{(0)}}、{W_{(0)}}を適当に初期化
  2. {t \leftarrow 0}
  3. {U_{(t+1)} \leftarrow \bar{X}^{vw}\left({V_{(t)}}^{T}V_{(t)} \circ {W_{(t)}}^{T}W_{(t)}\right)^{-1}}
  4. {V_{(t+1)} \leftarrow \bar{X}^{wu}\left({W_{(t)}}^{T}W_{(t)} \circ {U_{(t+1)}}^{T}U_{(t+1)}\right)^{-1}}
  5. {W_{(t+1)} \leftarrow \bar{X}^{uv}\left({U_{(t+1)}}^{T}U_{(t+1)} \circ {V_{(t+1)}}^{T}V_{(t+1)}\right)^{-1}}
  6. {t \leftarrow t+1}
  7. 収束するまで3-6を繰り返す

実装

入力データは X[(i,j,k)] = value という辞書で与える。fitで学習して、predictで予測する。self.A[i]にi次のモードに対応する潜在変数行列が入っている。

上の説明では正則化は入れてなかったけど、データによっては逆行列の計算でこける（特異行列）ので、実装ではL2正則化をいれてある。

あと、潜在変数行列は平均 0、分散 0.01 の正規分布で初期化した。

gist36b4c4c07e96e392f9c876ddcc84e7bc

実験

適当な潜在変数を予め用意して、それを使ってデータテンソルを作る。そんで、CP分解でそのテンソルを分解する。

fitすると、self._lossesに各イテレーション時のロスの値が入るので、それをプロットした。

適当に選んだ要素をちゃんとCP分解が復元できるかもためした（うまくいった）。

gist7b56d8330cd117f412b6798123cdb595

*1:3階にかぎらず一般のN階のテンソルに適用できる。

scikit-learn準拠で Label propagation とか実装した

machine learning python

scikit-learn準拠で Label propagation 的なアルゴリズム達を実装した。なんで実装したかというと、

  1. グラフそのもの（隣接行列）を入力したい。 scikit-learnには既にsklearn.semi_supervised.LabelPropagationが実装されてるけど、これはグラフを入力するんじゃなくて、普通にサンプル数×特徴数のデータ行列を与えて、そこから類似度グラフを作るようになってる。これだと例えば手元にソーシャルグラフがあって、そのユーザ（ノード）の属性（興味とか）を Label propagation で推定するということができない。
  2. ハイパーパラメータを楽に決めたい。 自分でグリッドサーチとかやるのはめんどくさいので、sklearn.grid_search.GridSearchCVとかを使いたい。そのためにsklearn準拠にした。
  3. 自分の研究成果を使いやすい形で公開したい。 AAAI15とSDM16でそれぞれラベル伝搬てきなアルゴリズムを提案したので、それを簡単に使えるようにした。

コード

github.com

使い方はREADME.mdに書いてあるけど、超ざっくり書くとこんな感じ。

from label_propagation import HMN
clf = HMN(graph=G) # Gは隣接行列（scipy.sparse）
clf.fit(x_train,y_train) # x_trainはラベル付きノードIDのリスト、y_trainは対応するノードのラベルのリスト
predicted = clf.predict(x_test) # x_testラベルを推定したいノードIDのリスト

あと、自分でpythonコードを書かなくても使えるようにmain.pyも書いた。例えばこうする（詳細はREADME）

$ python main.py lgc -g sample.edgelist -l sample.label -o outputfile --alpha 0.99

実装した手法

とりあえず以下の５つを実装した。他にも MAD [PKDD'09] とかもあるけど、それはまた今度。

Harmonic Function (HMN) [Zhu+, ICML'03]

Label propagationの始祖、全ての始まり。ハイパーパラメータが一つもない*1から簡単に使える反面、ラベルノイズに弱いという弱点がある。次のLGCと比較して、ラベルノイズがどーのこーのという話はこのへんに書いた

yamaguchiyuto.hatenablog.com

Local and Global Consistency (LGC) [Zhou+, NIPS'04]

HMNと比較するとラベルノイズに強い。でも、ラベルノイズをどの程度許容するかというパラメータが一つあるのでそれを調節する必要がある。Label propagation と言うと一般にこれを指すことが多い気がする。

Partially Absorbing Random Walk (PARW) [Wu+, NIPS'12]

PARWはノードの次数を考慮して、次数の小さいノードを超えてラベルが伝搬しないようにしている。次数の小さいノードは密なクラスタ間を接続するブリッジになっていることが多いので、こういうふうにするらしい*2。ただし、実世界のネットワーク（ソーシャルグラフとか）は次数分布がベキ分布に従っている（ハブがある）ことが多いため、そういう場合はうまくいかないと思う。

OMNI-Prop (OMNI) [Yamaguchi+, AAAI'15]

上記の三つの手法は、「隣同士のノードは同じラベルを持つ」という仮定をおいているため、「隣同士が異なるラベルを持つ」ようなグラフには適用できない。それに対してOMNIは隣同士が同じラベルを持つか異なるラベルを持つかをデータから勝手に判断してくれるのでどちらにも適用できる。詳細はこのへんに書いた

yamaguchiyuto.hatenablog.com

Confidence-Aware Modulated Label Propagation (CAMLP) [Yamaguchi+, SDM'16]

OMNIは隣同士がどういうラベルを持つかをデータから推定してくれるようになっているけど、当然データ（ラベル付きノード）が少ないときはうまくいかない。そこでCAMLPはあるラベルとあるラベルがどれくらいの確率で接続するかをパラメータとして指定する。パラメータは増えるが、適切にパラメータを決められれば強い。そういえばこの手法の紹介記事を書いてなかったからそのうち書こうかな（書かない）。

実装のポイント

  1. 上記の手法は全て F <- PF + B という行列演算の繰り返しに帰着する（CAMLPは少し例外）。Fはデータ数×ラベル数の行列で、各行に対応するデータが各ラベルを持つスコア（大きいほどそれっぽい）が入る。Pは遷移行列みたいなやつ。Bはそれぞれの手法で意味合いが少し違うけど、あらかじめ与えられたラベル（教師データ）が入る。なので、PとBを作ってやれば、あとは全ての手法で全く同じ行列演算をするだけになるから実装が簡単！
  2. scikit-learn準拠にするためには、fit(X,y)で学習、predict(X)で予測するようにしないといけない。なので、fitとかpredictに直接グラフ（隣接行列）を渡すことは出来ない。そこで、グラフはパラメータとして与えることにして、XとしてノードIDのリスト（データ数×１行列）、yとしてxに対応するノードのラベルを格納したリストを与えることにした。 つまり、Label propagationにおいては、グラフはパラメータで、特徴ベクトルはただのノードIDということになる。 scikit-learn準拠にするためにどうすれば良いかはこのへんに書いた

yamaguchiyuto.hatenablog.com

*1:類似度行列を作るときには類似度の定義やらなにやらに関するパラメータがあるけど、今回はグラフそのものを与えるので必要ない。

*2:はっきりとクラスタに分かれているようなユークリッド空間上のデータ点から類似度グラフを作った場合はこうなる。詳細は論文で。

TransE [NIPS'13] を実装（と実験再現）した

machine learning paper python

Graph embedding を調べる上で避けては通れないっぽいTransEを実装して実験再現してみた。モデルがシンプルでカッコイイし実装も簡単だった。データもパラメータも公開されてて実験を再現できたのもポイント高い。

TransE

NIPS'13で提案されたGraph embeddingをする手法。Google scholarで既に100以上引用されていろんな拡張モデルが提案されてる。論文は以下。

papers.nips.cc

TransEはKnowledge graph（Freebaseとか）をベクトル空間上にembeddingする。入力としてKnowledge graphを与えると、全てのsubject, predicate, objectに対してそれぞれk次元のベクトルを出力する。ポイントは出力されたベクトル空間に構造があること。例えば、

v(Kei Nishikori) + v(profession) = v(tennis player)*1

みたいな足し算ができるようになる*2。これは、("Kei Nishikori", "profession", "tennis player")というトリプルがある（ありそう）ということに対応している。

これの何が嬉しいかというと、例えばKnowledge graphのスキーマを意識しながらSPARQLを書いて問合せするっていうめんどくさいことをしなくても、単にベクトルの足し算をするだけで ("Kei Nishikori", "profession", ?) みたいな質問に答えられるようになる。もっと言うと ("Kei Nishikori", "profession", "tennis player") というトリプルがKnowledge graph上になくても、ベクトルの足し算をするだけで"tennis player"という答えを予測できるようになる。

学習

D = \{(h_i, r_i, t_i)\}_{i=1}^{n}というトリプルの集合（つまりKnowledge graph）が与えられた時、全てのトリプルについてできるだけ以下を満たすようにしたい：

{ \displaystyle v(h)+v(r) \simeq v(t) }

逆に、Dに含まれないトリプル（例えば ("Kei Nishikori", "profession", "politician") とか）については上記の足し算が成り立たないようにしたい。

これをどうやるかというと、まず、トリプルの "それっぽさ" を測る以下のスコア関数を定義する：

{ \displaystyle f(h,r,t) = ||v(h)+v(r)-v(t)|| }

右辺はノルムを表す。これは足し算が成り立つ時は0に近い値を取り、そうじゃない時は大きな値を取る。それっぽいトリプルは足し算が成り立つようにしたいので、このスコア関数が小さい値を取るように上手いことベクトルを割り当ててやる。逆に全然それっぽくないトリプルについてはこのスコア関数が大きな値を取るようにしたい。

うまいことベクトルを割り当ててやるには、以下の目的関数を最小化するようなベクトルを学習すれば良い*3：

{ \displaystyle L(V) = \sum_{(h,r,t) \in D} max(0, f(h,r,t) + \gamma - f(h',r,t')) }

f(h,r,t) が小さくて f(h',r,t') が大きければ全体として小さくなる（ガンマはマージンみたいな役割）。ここで (h',r,t') というトリプルが突然出てきてるんだけどこれがすごく重要な役割を果たす。Dには正例しか含まれない、つまりそれっぽくないトリプルは含まれないので、じゃあ人工的にそれっぽくないトリプルを作っちゃいましょうということで出てきたのが (h',r,t')。どうやって作るかというと、あるトリプル (h,r,t) に対して、hかtのいずれかを、ランダムに取ってきたentity（h'もしくはt'）と交換する。つまり一つのトリプル (h,r,t) にたいして一つの "それっぽくない" トリプル (h',r,t')を作る。こうすることで正例と負例の両方を使って学習することができるようになる*4。

上記の目的関数の最小化には mini-batch SGD を使う。勾配は単に（L1 or L2）ノルムを微分すれば良い。

実装

transe.pyが本体で、それ以外は論文の実験を再現するためのスクリプト。注意するポイントは特に無さそう。論文に書いてあるとおりに実装できる（えらい）。論文にはearly stoppingしたほうが良いよって書いてあったけどそこだけ無視した（あんまり変わらない）。

Reproducing TransE experiments NIPS'13

実験

論文に書いてある実験結果を部分的に再現してみた。データもパラメータもちゃんと公開されててすばらしい。

データはここで公開されてるFB15kをつかった。これはFreebaseからサンプルされた15,000エンティティを含むデータ。割りと小さいけど評価実験するくらいならこれくらいでいいのかな。

まずデータを用意する。

% wget 'https://everest.hds.utc.fr/lib/exe/fetch.php?media=en:fb15k.tgz'
% mv fetch.php\?media=en:fb15k.tgz fb15k.tgz
% tar zxvf fb15k.tgz

学習する。パラメータは論文に書いてあるとおり。SGD は mini-batch の size を5000で 1000 epochs 回した*5。標準出力に表示されている 10 1528.218 みたいなのは 10 epochs 回した直後の validation set での mean rank の値を表している（Mean rankについては後述）。結果として学習されたモデルが "transe.model" というファイルに書き出される（pickle）。

% python train.py FB15k/freebase_mtr100_mte100-train.txt FB15k/freebase_mtr100_mte100-valid.txt
0 3560.291
10 1528.218
.
.
.
990 198.681

論文中の実験を再現する前に少し遊んでみる。predict.pyに 予測したいトリプル (h,r,?) を入力するとそれっぽい t を上位 n 件返してくれる。使用したデータセットはエンティティをFreebaseのmidで管理してるのでわかりづらいんだけど、"/m/051q39/"は有名なテニスプレイヤーの Rafael Nadal を表していて、以下の例ではそれのnationalityを知りたいということになる。

% python predict.py transe.model /m/051q39  /people/person/nationality 10
/m/0b1t1        7.87806854062
/m/0d04z6       8.14848562699
/m/06mkj        8.1821732884
/m/03rk0        8.24374933051
/m/027rn        8.27577702421
/m/0hzlz        8.2857627988
/m/0160w        8.31141651263
/m/015fr        8.37179251603
/m/05r4w        8.4572799401
/m/04g5k        8.4820680158

結果としてFreebaseのmidが出てくるので非常にわかりづらいんだけど、top3は"London", "Cuba", "Spain"となった。正しいnationalityはスペインなので、まあそれなりの結果なのかな。右の列の数値はスコア関数の値で、結果はこの値でソートされている（小さいほどそれっぽい）。ちなみに ("Rafael Nadal", "nationality", "Spain") というトリプルは学習データに含まれていないので、上手いこと正しいトリプルを予測できたことになる。データセットが小さいのであまりおもしろい結果は出ないんだけど、色々試してみるといいかも。

さてさて、論文中の実験を再現する。論文中ではMeanRankとHit10という二つの評価尺度が使われている。MeanRankというのは ("Kei Nishikori", "profession", ?) みたいなトリプルを入力した時に正しい答え "tennis player" が予測されたランクを全てのテストトリプルについて平均をとったもの。小さいほどよい。Hit10というのは同じくテストトリプルを入力した時に正しい答えが上位10位以内に予測された割合。大きいほどよい。

% python test.py transe.model FB15k/freebase_mtr100_mte100-test.txt
MeanRank: 190.301450796
Hit10: 0.417192869598

論文中ではMeanRankが243、Hit10が34.9になってるのでそれより結構良い結果が出ちゃったけどまぁいいでしょうということで。

まとめ

とにかくシンプル。ムダなところを一切削ぎ落としたようなモデルでカッコイイね。ただシンプル過ぎてこれでうまくいくのかよという感もある。実際TransEではうまくいかない例もいくつもあって、後続の（他の人が提案した）いろんなモデルで修正されてる。ただ後続の手法も枠組みはTransEとほぼおなじで、おおまかに言えばスコア関数 f を変えてるだけ。たくさんの人に使ってもらうには surprisingly simple and moderately effective なものを作るのが重要だといういい例だった。

*1:v(.)は埋め込まれたベクトルを表す

*2:ちょっと前にかなり話題になったword2vecっぽいし、論文中にもinpired by word2vecと書いてある。

*3:論文中の表記はわかりづらいので変更してある

*4:Negative samplingと言う。

*5:なぜかmini-batch sizeをどうしたかだけ論文中に記載がなかった。