Robust Large-Scale Machine Learning in the Cloud [KDD'16] を読んだ
KDD16で発表されてた論文。著者はかの有名なFactorization Machinesの人。Googleに行ってたのね。いままでとはちょっと違う研究をしてるように感じる。
論文はここから読める。
勉強会で紹介したので念のため、その時のスライドはこちら。
一言まとめ
一般化線形モデルの学習を Coordinate Descent で、めっちゃスケールさせるよ。
概要
Coordinate Descent (CD) はシングルマシン上では収束が早いアルゴリズムとして知られてるんだけど、分散には向かない。なぜなら、アルゴリズムの特性上、分散させると1つのワーカーに割り当てられる work load が小さくなってしまって、オーバヘッドを考えると分散効果が小さいから。CDはパラメータの更新を次元ごとに 逐次 繰り返していくことで収束するアルゴリズムなので、分散させるには基本的にはデータパラレルにすることになる。でもパラメータの1つの次元を更新するときの処理はそんなに重くないので、分散させるメリットがあまりないということ。
そこでこの論文では1つの次元ごとじゃなくて、次元の集合(ブロック)ごとに更新するのをくりかえす Scalable Coordinate Descent (SCD) というアルゴリズムを提案する。そうすることで分散させて1つのワーカーに割り当てる work load をある程度大きくすることが出来る。で、ブロックごとに更新しても収束するのか? という話だけど、パラメータの更新時にこれまでの値と更新後の値の間で line search してやると収束するらしい。なぜかは知らん(書いてない)。さらに、特徴次元をうまいことブロックに分割しれやれば、CDと全く同じ解が得られることも示した。
で、この SCD を Google Cloud 上に実装したらしい。論文中では実装時の細かいところの説明がされていた。この辺もさらっと書いてあるけどいろいろ試行錯誤して大変だったんだろなと思った。ポイントは、VM Preemptionがある環境を想定しているところなのかな? AWS の Spot instance とかがそれなんだけど、優先度が低いとみなされた VM(=worker) が勝手に強制終了されて、空いたリソースが別の優先度の高いVMに割り当てられてしまうという環境。
実際にGoogleが持ってる広告のデータを使って実装したらしい。サンプル数は1兆(!)で、特徴数は10億(!)のスケールのデータらしい。Google恐るべし。ちなみにこれはNetflix prizeの1万倍の規模らしい。結果はここでは省略するけどスケールしたとのこと。
無限潜在特徴モデルを実装した
引き続きノンパラベイズ。今回はノンパラベイズ本の7.4節で説明されてる無限潜在特徴モデル(Infinite latent feature model; ILFM)を実装した。

ノンパラメトリックベイズ 点過程と統計的機械学習の数理 (機械学習プロフェッショナルシリーズ)
- 作者: 佐藤一誠
- 出版社/メーカー: 講談社
- 発売日: 2016/04/20
- メディア: 単行本(ソフトカバー)
- この商品を含むブログを見る
無限潜在特徴モデル
一言で言えば、潜在次元に無限次元を仮定する行列分解。
与えられたデータ行列 をバイナリ行列
と特徴行列
の積に分解する。
バイナリ行列の要素 はサンプル n が k 番目の潜在特徴を持つか持たないかを表している。k番目の潜在特徴は
のk番目の行ベクトル
で表されている。つまり、あるサンプルのデータベクトル
は無限個ある潜在特徴のうちのいくつかの和になっている。
通常の行列分解では分解後の行列の潜在次元数 K を予め決めなきゃいけないんだけど、このモデルはノンパラベイズなので決めなくて良い。データから勝手に決まる。さすがノンパラベイズ。
モデルの説明とパラメータ推定の説明は上の本に詳しく書いてあるので割愛。
実装
特に注意すべき点はないと思うけど、強いて言うならサンプリングの事後分布を計算するときにunderflowしないように対数のまま正規化してやるくらい。
実験
alphaを小さく設定してもどうしても真のKより大きな潜在次元数が推定されてしまう。何か間違ってるのかこういうもんなのか判断ができない。相対誤差は十分(?)小さくなってる。
無限混合ガウスモデルを実装した
ノンパラベイズ面白いね。佐藤一誠先生のノンパラメトリックベイズの本を読んで自分なりに理解できたので実装してみた。本読んで理解して、自分で導出して、実装・実験するの本当に重要。定着度がぜんぜん違う。

ノンパラメトリックベイズ 点過程と統計的機械学習の数理 (機械学習プロフェッショナルシリーズ)
- 作者: 佐藤一誠
- 出版社/メーカー: 講談社
- 発売日: 2016/04/20
- メディア: 単行本(ソフトカバー)
- この商品を含むブログを見る
無限混合ガウスモデルは上の本の5.2節で説明されてるモデルで、ディリクレ過程混合ガウスモデル(Dirichlet Process Gaussian Mixture Model; DPGMM)とも呼ぶらしい。面倒くさいので以下DPGMMと書く。
DPGMM
普通の混合ガウスだと分割数(クラスタの数)K を事前に決めなきゃいけないんだけど、これが面倒くさいし、よほどそのデータに詳しいか超能力でも無い限り、いろんな K の値を試してみないといけない。面倒くさい。
そこでDPGMMの出番。予め K を決めなくてもデータから推定してくれる。便利。
感覚的にちょっと説明すると、あるデータ点のクラスタ割り当てを決めるとき、普通の混合ガウスだったらそのデータ点を生成したっぽいクラスタ(ガウシアン)に割り当てるんだけど、DPGMMだとどのクラスタからも生成されたっぽくないときは新しいクラスタが作られる。このクラスタ割り当てを何度も何度もやる(ギブスサンプリング)ことで、最終的に適切な数のクラスタが作られ、全てのデータ点が適切なクラスタに割り当てられる。
詳細は上の本を読むと良い。佐藤先生の本は本当に超わかりやすい。
実装
めっちゃ遅いけど実装した。本に書いてあるように、共分散行列は対角行列と仮定した。
Dirichlet Process Gaussian Mixture Model
実験
真のクラスタ数は3で、分散は全てのクラスタで1。クラスタ間が互いにかなり離れてるので簡単な設定になってる。
結果を見ると、クラスタ数を指定してないのに、クラスタが3つ作られて、全てのデータ点が適切なクラスタに割り当てられていることが分かる。
Tucker分解の導出と実装
CP分解の次はTucker分解を導出して実装する。丁寧にTucker分解の導出を説明してる文献(Web含め)が全然なかったので、自分で書く。CP分解についてはある程度知ってる前提とする。CP分解についてはこちらから。
まとめ
- Tucker分解とは
- ALSでTucker分解の更新式の導出
- PythonでTucker分解を実装
- 人工データを使って実験
Tucker分解とは
Tucker分解は、テンソルを1つのテンソル(コアテンソルと呼ぶ)と、それぞれのモードに対して一つずつの行列に分解する。
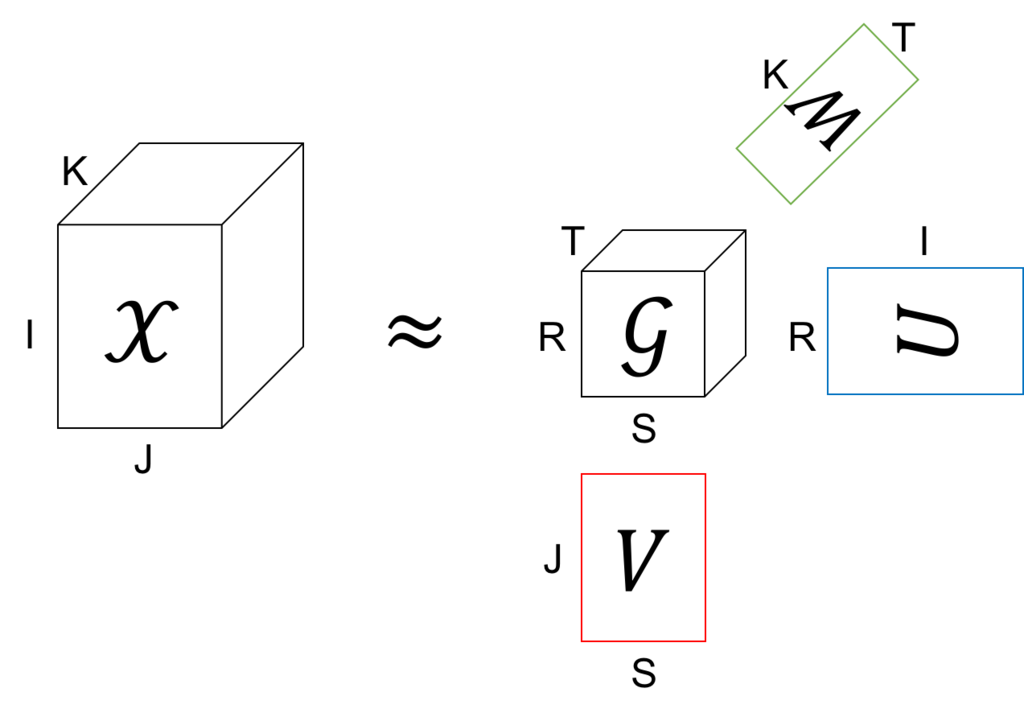
上の図の例では、もとのテンソルのサイズは IxJxK だけど、これをコアテンソルのサイズの RxSxT (R<=I, S<=J, T<=K) まで小さくしている。また、あとで説明するけど、行列 U、V、W は全て直行行列となるように分解する。このコアテンソル と3つの直交行列を使ってもとのテンソル
を近似する。
これを式で書くと、
という分解をしていることになる。
この分解が何かに似ていると思った人はお目が高い。実は、コアテンソルが対角要素が全部1の対角テンソルのとき、Tucker分解はCP分解と等しくなる。つまり、CP分解はモデル的にはTucker分解の特殊ケースということになる。
ALSでTucker分解の更新式の導出
上で説明したように、Tucker分解ではテンソル を1つのコアテンソル
と、(テンソルが3階の場合は)3つの直交行列
、
、
に分解する。分解の方針はCP分解のときと同じで、ALS (Alternating Least Square) で行く。
さて、以下のコスト関数を最小にすることを考える。
これはただ単にテンソル の全要素について近似誤差の和の二乗を取っているだけ。ただし、問題を簡単にするために
、
、
は直交行列であるとする。
L を で微分すると
ここで、 は直交行列だから、
のとき
、また
のとき、
となる。よって、
これを 0 と置いて について解くと、
となる。これを★とする。
★を L に代入するが、その前にまず L をちょっと変形すると
ここで、第二項を変形して★を代入すると、
また第三項に★を代入すると、
ここでまた が直交行列なので、
かつ
かつ
のときの項のみが残って、
となる。
まとめると、Lは以下のように書ける。
結局、L を最小化するという問題は、、
、
が直行という制約のもとで
を最大化するという問題に帰着した(やっとスタート地点に立った・・・)。これを L' と置こう。
さて、ALSなので、 と
を固定して、L' を最大化する
を求める。
今後の見通しを良くするために L' をちょっと変形する、
ここで と置くと、
また、添字 s と t をまとめて q と書くと*1、
ここで、、
とした。すべての
は独立に考えられるから、ある
について
の制約のもとで L' を最大化する。
とおいて、 で微分すると、
と置くと、
これを 0 と置くと、
つまり、 は 行列
の固有ベクトル、また行列
の左特異ベクトルということになる。
この を全ての r について互いに直交するように求めれば良いから、結局行列
を特異値分解して得られる左特異ベクトルが答えとなる。
長かった・・・。
と
についても同様に求まる。まとめると、
、
、
を適当に初期化する
を 特異値分解し、左特異ベクトルを
とする
を 特異値分解し、左特異ベクトルを
とする
を 特異値分解し、左特異ベクトルを
とする
- 収束するまで 2-6 を繰り返す。
- ★により
を求める。
実装
scipy.sparse は疎テンソルを扱えないので、データテンソルは X[(indices)]=value という辞書で与えた。indicesはインデックスが入ったタプル。
gist74f1026096be91ba0a147eeaa540326c
実験
平均0、標準偏差1の正規分布でコアテンソル と直交行列 U、V、W を初期化し、データテンソル
を作って、平均0、標準偏差0.1の正規ノイズを加えた。
Tucker分解が真のコアテンソル と直交行列 U、V、W を復元できるか試した。
max_iter=5 としたけど、一回で(ほぼ)収束した。収束するまで特異値分解し続けるのがHOOI、一回だけ特異値分解するのがHOSVDと呼ばれてるけど、この例ではHOSVDで十分っぽい。
学習した後に残差(の平均)を見てみたけど十分小さいのでOK。
gist86035070f286f595f3f1078ed2002e3a
*1:q = s*T + t とすればよい
クロネッカー積とvec作用素とRoth's column lemma
クロネッカー積とvec作用素は見た目簡単なんだけど、各要素のインデックスを書き下すと頭の中こんがらがってわけわからなくなるから一旦整理した。インデックスに関する記事ってほとんどないね。あとそれに関連して Roth's column lemma っていうのが便利なのでちょっと紹介する。
まとめ
クロネッカー積とは
下の式を見ればひと目で分かるけど、 IxJ 行列 と KxL 行列
から IKxJL 行列を作る。
Wikipediaの例を見ると分かりやすい。
クロネッカー積のインデックス
クロネッカー積の定義は一目見ればすぐ分かるのに、各要素の定義を見ると途端にめんどくさくなる。
行のインデックスを見ると、K進数みたいになってるのが分かる。 の行のインデックスが1つ増えるためには、
の行のインデックスを一回ずつ辿らなきゃいけないって考えるとそうなることが分かる。列についても同じ。
実験
上式のインデキシングが本当に合ってるのか numpy.kron を使って確かめる。
gist6cf39c77df3bf44fe6ed5aaf98c343cc
vec作用素
vec作用素は、以下のように IxJ 行列 の列ベクトルを全て一列に並べて1つの大きな IJ 次元列ベクトルを作る。
例えば、以下のようになる
vec作用素のインデックス
こっちはクロネッカー積よりは簡単。
クロネッカー積のときと同じで、J進数みたいになってる。各列ベクトルがJ次元なので、 の
が増えるためには
を全部辿らなきゃならない。
Roth's column lemma
これが成り立つ。
証明
をIxJ行列、
をJxK行列、
をKxL行列とし、
と置く。 は IxL 行列。
の各要素は(とうぜん)以下のように書ける。
クロネッカー積の要素を考えると
vec作用素の要素を考えると
なので、以下の行列ベクトル積の要素を考えると、
だから、証明完了。
