Tucker分解の導出と実装
CP分解の次はTucker分解を導出して実装する。丁寧にTucker分解の導出を説明してる文献(Web含め)が全然なかったので、自分で書く。CP分解についてはある程度知ってる前提とする。CP分解についてはこちらから。
まとめ
- Tucker分解とは
- ALSでTucker分解の更新式の導出
- PythonでTucker分解を実装
- 人工データを使って実験
Tucker分解とは
Tucker分解は、テンソルを1つのテンソル(コアテンソルと呼ぶ)と、それぞれのモードに対して一つずつの行列に分解する。
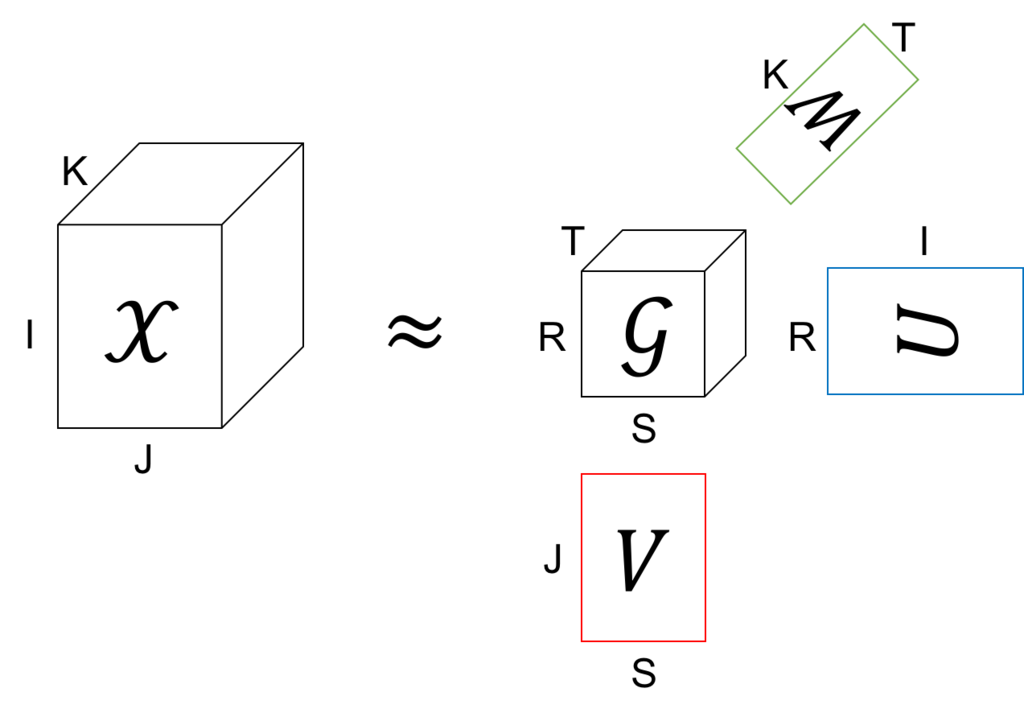
上の図の例では、もとのテンソルのサイズは IxJxK だけど、これをコアテンソルのサイズの RxSxT (R<=I, S<=J, T<=K) まで小さくしている。また、あとで説明するけど、行列 U、V、W は全て直行行列となるように分解する。このコアテンソル と3つの直交行列を使ってもとのテンソル
を近似する。
これを式で書くと、
という分解をしていることになる。
この分解が何かに似ていると思った人はお目が高い。実は、コアテンソルが対角要素が全部1の対角テンソルのとき、Tucker分解はCP分解と等しくなる。つまり、CP分解はモデル的にはTucker分解の特殊ケースということになる。
ALSでTucker分解の更新式の導出
上で説明したように、Tucker分解ではテンソル を1つのコアテンソル
と、(テンソルが3階の場合は)3つの直交行列
、
、
に分解する。分解の方針はCP分解のときと同じで、ALS (Alternating Least Square) で行く。
さて、以下のコスト関数を最小にすることを考える。
これはただ単にテンソル の全要素について近似誤差の和の二乗を取っているだけ。ただし、問題を簡単にするために
、
、
は直交行列であるとする。
L を で微分すると
ここで、 は直交行列だから、
のとき
、また
のとき、
となる。よって、
これを 0 と置いて について解くと、
となる。これを★とする。
★を L に代入するが、その前にまず L をちょっと変形すると
ここで、第二項を変形して★を代入すると、
また第三項に★を代入すると、
ここでまた が直交行列なので、
かつ
かつ
のときの項のみが残って、
となる。
まとめると、Lは以下のように書ける。
結局、L を最小化するという問題は、、
、
が直行という制約のもとで
を最大化するという問題に帰着した(やっとスタート地点に立った・・・)。これを L' と置こう。
さて、ALSなので、 と
を固定して、L' を最大化する
を求める。
今後の見通しを良くするために L' をちょっと変形する、
ここで と置くと、
また、添字 s と t をまとめて q と書くと*1、
ここで、、
とした。すべての
は独立に考えられるから、ある
について
の制約のもとで L' を最大化する。
とおいて、 で微分すると、
と置くと、
これを 0 と置くと、
つまり、 は 行列
の固有ベクトル、また行列
の左特異ベクトルということになる。
この を全ての r について互いに直交するように求めれば良いから、結局行列
を特異値分解して得られる左特異ベクトルが答えとなる。
長かった・・・。
と
についても同様に求まる。まとめると、
、
、
を適当に初期化する
を 特異値分解し、左特異ベクトルを
とする
を 特異値分解し、左特異ベクトルを
とする
を 特異値分解し、左特異ベクトルを
とする
- 収束するまで 2-6 を繰り返す。
- ★により
を求める。
実装
scipy.sparse は疎テンソルを扱えないので、データテンソルは X[(indices)]=value という辞書で与えた。indicesはインデックスが入ったタプル。
gist74f1026096be91ba0a147eeaa540326c
実験
平均0、標準偏差1の正規分布でコアテンソル と直交行列 U、V、W を初期化し、データテンソル
を作って、平均0、標準偏差0.1の正規ノイズを加えた。
Tucker分解が真のコアテンソル と直交行列 U、V、W を復元できるか試した。
max_iter=5 としたけど、一回で(ほぼ)収束した。収束するまで特異値分解し続けるのがHOOI、一回だけ特異値分解するのがHOSVDと呼ばれてるけど、この例ではHOSVDで十分っぽい。
学習した後に残差(の平均)を見てみたけど十分小さいのでOK。
gist86035070f286f595f3f1078ed2002e3a
*1:q = s*T + t とすればよい